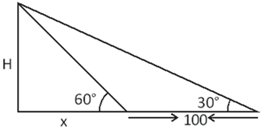
Question

A vertical tower subtends an angle of $60^{o}$ at a point on the same level as the foot of the tower. On moving $100m$ further from the first point in line with the tower, it subtends an angle of $30^{o}$ at the point. If the height of the tower is $Hm$ , then the value of $\frac{H}{25 \sqrt{3}}$ (in meters) is

Answer 1

$tan 60^{o}=\frac{H}{x},tan⁡30^{o}=\frac{H}{x + 100}$
$\Rightarrow $ $\frac{H}{t a n 6 0^{^\circ }}=\frac{H}{t a n 3 0^{^\circ }}-100$
$\Rightarrow $ $\frac{H}{\sqrt{3}}=\frac{H}{1/\sqrt{3}}-100$
$\Rightarrow $ $\sqrt{3}H-\frac{H}{\sqrt{3}}=100\Rightarrow 3H-H=100\sqrt{3}$
$\Rightarrow H=50\sqrt{3}$
$\frac{H}{25 \sqrt{3}}=2$