Question

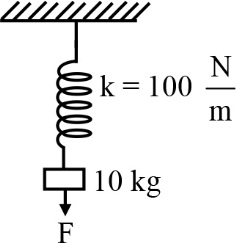
A vertical spring of force constant $100 \, Nm^{- 1}$ is attached with a hanging mass of $10kg$ . Now an external force is applied on the mass so that the spring is stretched by an additional $2m$ . The work done by the external force is : ( $g=10 \, ms^{- 2}$ )

• A. $200 \, J$
• B. $400 \, J$
• C. $450 \, J$
• D. $600 \, J$

Answer 1

Answer: (A)

At equilibrium, $mg=k x_{0} \, \Rightarrow x_{0}=\frac{m g}{k}=1 \, m$




$\therefore W=U_{2} \, - \, U_{1}$
$=\frac{1}{2} \, kx_{2}^{2}- \, \left[\frac{1}{2} \, k x_{1}^{2} + m g h\right]$
$=\frac{1}{2} \, k \, \left(x_{2}^{2} \, - \, x_{1}^{2}\right) \, - \, mgh$
$=\frac{1}{2} \, \times \, 100 \, \times \, \left(3^{2} \, - \, 1^{2}\right) \, - \, 10 \, \times \, 10 \, \times \, 2=200 \, J$