1. Tardigrade
  2. Question
  3. Physics
  4. A vector Q has a magnitude of 8 is added to the vector p which ties along the X-axis. The resultant of these two vectors is a third vector R which lies along the Y-axis and has a magnitude twice that of P The magnitude of P is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

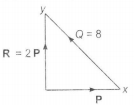
Q. A vector $Q$ has a magnitude of 8 is added to the vector $p$ which ties along the X-axis. The resultant of these two vectors is a third vector $R$ which lies along the Y-axis and has a magnitude twice that of $P$ The magnitude of $P$ is

EAMCETEAMCET 2003Motion in a Plane

Solution:

Given Q = 8 units
$ R = 2 P$
Since. R is along Y-axis and P is along x-axis.
Therefore. P and R are perpendicular vectors.
Hence, $ Q^2 = R^2 + P^2$
Putting the given values in Eq. (i), we get
$ (8)^2 = (2P)^2 + P^2 = 4P^2 + P^2 = 5 P^2 \, \, \, or \, \, \, 5 P^2 = 64$
$ P^2 = \frac{64}{5}$
$\therefore P = \frac{8}{\sqrt5}$

Solution Image