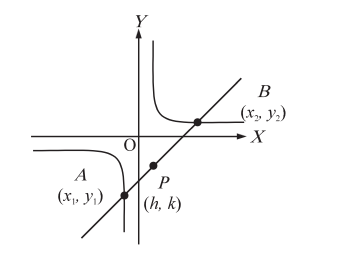
Question

A variable straight line of slope 4 intersects the hyperbola $x y=1$ at two points. The locus of the point which divides the line segment between these two points in the ratio $1: 2$ is

• A. $16 x^{2}+10 x y+y^{2}=2$
• B. $16 x^{2}-10 x y+y^{2}=2$
• C. $16 x^{2}+10 x y+y^{2}=4$
• D. none of these

Answer 1

Answer: (A)

Let $P(h, k)$ be any point on the locus. Equation of the line through $P$ and having slope $4$ is

$y-k=4(x-h) ...$(1)
Suppose, this line meets $x y=1 ...$(2)
in $A\left(x_{1}, y_{1}\right)$ and $B\left(x_{2}, y_{2}\right)$
Eliminating $y$ from (1) and (2), we get
$\frac{1}{x}-k=4(x-h) $
$\Rightarrow 4 x^{2}-(4 h-k) x-1=0...$(3)
Since $x_{1}$ and $x_{2}$ are the roots of $(3)$
$\therefore x_{1}+x_{2}=\frac{4 h-k}{4}....$(4)
and, $x_{1} x_{2}=\frac{-1}{4} ....$(5)
Also, $\left(\frac{8 h+k}{2}\right)\left(-\frac{2 h+k}{2}\right)=-\frac{1}{4}=h$
or $2 x_{1}+x_{2}=3 h....$ (6)
From (4) and (6), we get
$x_{1}=3 h-\frac{(4 h-k)}{4}=\frac{8 h+k}{4}$
and, $x_{2}=3 h-\frac{(8 h+k)}{2}=\frac{-(2 h+k)}{2}$
Putting these values in (5), we get
$\left(\frac{8 h+k}{2}\right)\left(-\frac{2 h+k}{2}\right)=-\frac{1}{4} $
$\Rightarrow (8 h+k)(2 h+k)=2$ or $ 16 h^{2}+10 h K+k^{2}=2$
Thus, equation of required locus is
$16 x^{2}+10 x y+y^{2}=2$.