Question

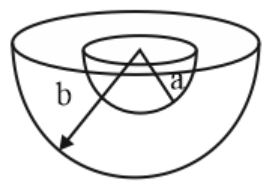
A uniformly charged hemisphere of radius $b$ and charge density $\rho $ has a hemispherical cavity of radius $a\left(a = \frac{b}{2}\right)$ cut from its centre. If the potential at the centre of the cavity is $\frac{n \rho b^{2}}{16 \in _{0}}$ then $n=?$

• A. 3
• B. 4
• C. 5
• D. 6

Answer 1

Answer: (A)

$V=\displaystyle \int _{a}^{b} \frac{K \left(2 \pi x^{2} d x\right) \rho }{x}$
$V=2\pi k\rho \left[\frac{b^{2} - a^{2}}{2}\right]=\pi \rho k\left(b^{2} - a^{2}\right)$
$b=2a$
$v=3\pi k\rho b^{2}$