Question

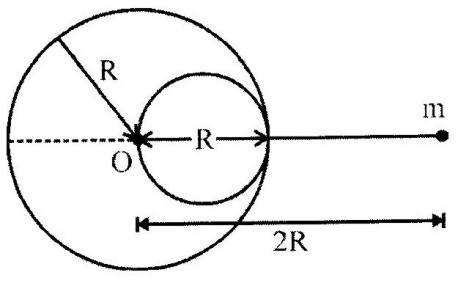
A uniform sphere (mass $M$ , radius $R$ ) exerts a force $F$ on a small mass $m$ placed at distance $2R$ from the centre of the sphere. A sphere of radius $\frac{R}{2}$ is excavated from the sphere as shown in the figure. Find the force applied by the remaining part of the sphere on the point mass.

• A. $\frac{F}{3}$
• B. $\frac{4 F}{9}$
• C. $\frac{2 F}{3}$
• D. $\frac{7 F}{9}$

Answer 1

Answer: (D)

The mass of the sphere $M=\frac{4}{3}\pi R^{3}\rho $ where $\rho $ is the density.
The force of attraction between the sphere and the mass m is
$F=\frac{G M m}{\left(2 R\right)^{2}}=\frac{G M m}{4 R^{2}}$ ... (1)
Mass of the cut out sphere is $m′=\frac{4}{3}\pi \left(\frac{R}{2}\right)^{3}\rho =\frac{1}{8}\left[\frac{4}{3} \pi R^{3} \rho \right]=\frac{1}{8}\left(M\right)$
The force of attraction between the cut out portion and 'm'.
$f=\frac{G m ′ m}{\left(\frac{3 R}{2}\right)^{2}}$ $\because $ $O′P=2R-\frac{R}{2}=\frac{3 R}{2}$
$=\frac{G \left(\frac{M}{8}\right) \cdot m}{\frac{9 R^{2}}{4}}=\frac{G M m}{2 \times 9 R^{2}}$
$=\left(\frac{G M m}{4 R^{2}}\right)\times \frac{2}{9}=\frac{2}{9}F$ ... from (1)
$\therefore $ The force of attraction between the remaining portion and $m=F-\frac{2}{9}F=\frac{7}{9}F$ .