Q.
A uniform solid sphere rolls down a vertical surface without sliding. If the vertical surface moves with an acceleration $a=\frac{g}{2}$, If the minimum coefficient of friction between the sphere and vertical surfaces so as to prevent relative sliding is found to be $\frac{n}{7}$. The value of $n$ is ____.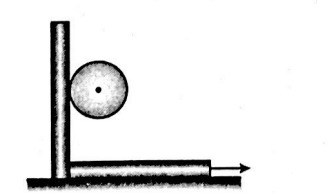
System of Particles and Rotational Motion
Solution:
