Q.
A uniform solid sphere of radius $r=\frac{R}{5}$ is placed on the inside surface of
a hemispherical bowl with radius $R(=5 r)$. The sphere is released from rest at an angle $\theta=37^{\circ}$ to the vertical and rolls without slipping (Fig.). The angular speed of the sphere when it reaches the bottom of the bowl is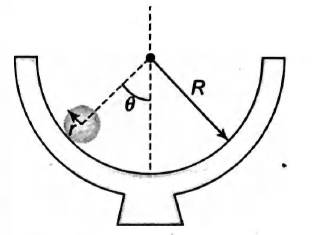
System of Particles and Rotational Motion
Solution:
