Q.
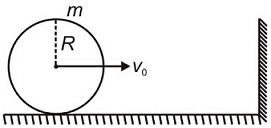
A uniform solid sphere of mass $m$ , radius $R$ moving with velocity $v_{0}$ is rolling without slipping on a frictionless surface. It collides elastically with a frictionless vertical wall. Ratio of magnitude of angular momentum of the sphere before and after the collision about its bottommost point is
NTA AbhyasNTA Abhyas 2020System of Particles and Rotational Motion
Solution: