Q.
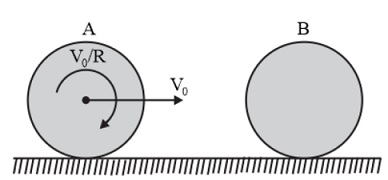
A uniform solid sphere $A$ of mass $m$ is rolling without sliding on a smooth horizontal surface. It collides elastically and head-on with another stationary hollow sphere $B$ of the same mass and radius. Assuming friction to be absent everywhere, the ratio of the kinetic energy of $B$ to that of $A$ just after the collision is
NTA AbhyasNTA Abhyas 2020System of Particles and Rotational Motion
Solution: