Question

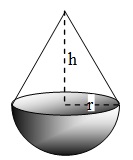
A uniform solid right circular cone of the base radius $r$ is joined to a uniform solid hemisphere of radius $r$ and of the same density, so as to have a common face. The centre of mass of the composite solid lies on the common face. The height of the cone is

• A. $2 \, r$
• B. $\sqrt{3}r$
• C. $3 \, r$
• D. $\sqrt{6}r$

Answer 1

Answer: (B)

Volume of cone $=\frac{1}{3}\pi r^{2}h$
Mass of cone, $m_{1}=\rho \times \frac{1}{3}\pi r^{2}h$
Mass of hemisphere, $m_{2}=\rho \times \frac{1}{2}\times \frac{4}{3}\pi r^{3}$
$=\rho \times \frac{2}{3}\pi r^{3}$

Now, $Y=\frac{m_{1} y_{1} + m_{2} y_{2}}{m_{1} + m_{2}}$
$\Rightarrow 0=\frac{\rho \times \frac{1}{3} \pi r^{2} h \times \frac{h}{4} + \frac{2}{3} \pi r^{3} \left(\right. - \frac{3 r}{8} \left.\right)}{\rho \times \frac{1}{3} \pi r^{2} h + \rho \times \frac{2}{3} \pi r^{2}}$
$\Rightarrow \rho \times \frac{1}{3}\pi r^{2}\left(\frac{h^{2}}{4} - 2 r \times \frac{3 r}{8}\right)=0$
$\frac{h^{2}}{4}-\frac{3 r^{2}}{4}=0 \, $
or $h=\sqrt{3} \, r$