Q.
A uniform solid disk of radius $R$ and mass $M$ is free to rotate on a frictionless pivot through point on its rim. If the disk is released from rest in the position shown in figure. The speed of the lowest point on the disk in the dashed position is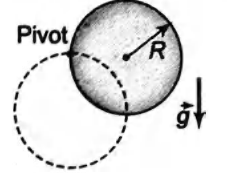
System of Particles and Rotational Motion
Solution:
