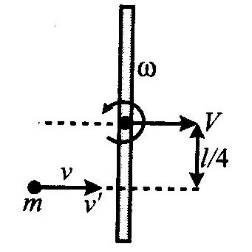
Question

A uniform smooth rod (mass $m$ and length $l$ ) placed on a smooth horizontal floor is hit by a particle (mass $m$ ) moving on the floor, at a distance $\frac{l}{4}$ from one end elastically ( $e=1$ ). The distance travelled by the centre of the rod after the collision, when it has completed three revolutions, will be

• A. $2\pi l$
• B. $3\pi l$
• C. $\pi l$
• D. $4\pi l$

Answer 1

Answer: (A)

Applying conservation of linear momentum,
$mv=mv′+mV$
$\Rightarrow v=v′+V$ ........(i)
Applying conservation of angular momentum about the point of collision
$0=\left(\frac{m l^{2}}{12}\right)\omega -mV\left(\frac{l}{4}\right)$
$\Rightarrow l\omega =3V$ ..........(ii)
for a perfectly elastic collision $e=1$
$v-0=V+\frac{\omega l}{4}-v′$ ..........(iii)
$v=V+\frac{3 V}{4}-\left(v - V\right)$
$2v=\frac{11 V}{4}$
$\Rightarrow V=\frac{8 v}{11}$
$\omega =\frac{24 v}{11 l}$
Angle rotated by the rod $\theta =6\pi $
$t=\frac{\theta }{\omega }=\frac{6 \pi }{\omega }$
$t=6\pi \times \frac{11 l}{24 v}=\frac{11 l}{4 v}$
Hence, distance travelled by the centre of the rod is
$S=Vt$
$S=\frac{8 v}{11}\left(\frac{11 l}{4 v}\right)=2\pi l$