Question

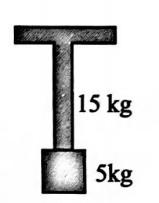
A uniform rope of length 10 cm and mass 15 kg hangs vertically from a rigid support. A block of mass 5kg is attached to the free end of the rope. A transverse pulse of wavelength 0.08 m is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope will be:

• A. 0.08 m
• B. 0.04 m
• C. 0.16 m
• D. 0 m

Answer 1

Answer: (C)

Velocity at lower end,
$V_{1}=\sqrt{\frac{50 \times 10 \times 10^{-2}}{15}}$
$\lambda_{1}=0.08 m$
$f_{1}=\frac{V_{1}}{\lambda_{7}}$
Velocity at upper and
$=V_{2}=\sqrt{\frac{200 \times 10 \times 10^{-2}}{15}}$
$f_{2}=\frac{V_{2}}{\lambda_{2}} ; f_{1}=f_{2}$
$\sqrt{\frac{50 \times 10 \times 10^{-2}}{15}}$ ;
$\lambda_{2}=\sqrt{\frac{200 \times 10 \times 10^{-2}}{15}} \times 0.08$
$\sqrt{50} \times \lambda_{2}=\sqrt{200} \times 0.08$
$\lambda_{2}=2 \times 0.08$
$\lambda_{2}=0.16 m$