Question

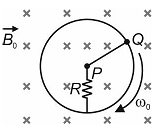
A uniform rod $PQ$ of length $l$ and mass $m$ is placed on a smooth horizontal surface. It is hinged at one of its ends and touches the conducting circular loop at another end. The system is subjected to vertical magnetic field B₀. Rod is given angular velocity $\omega _{0}$ about the axis passing through $P$ . If the time after which its angular velocity becomes half is $\frac{a}{b}\frac{m R \text{l} n 2}{B^{2} l^{2}}$ . Find the value of $\left(a + b\right)$ , where $a$ and $b$ are smallest positive integers.

Answer 1

$\epsilon =\frac{1}{2}B_{0}\omega l^{2}$
$I=\frac{1}{2}\frac{B_{0} \omega l^{2}}{R}$
$\tau=\frac{I l^{2} B_{0}}{4}=\frac{1}{4}\frac{B_{0} \omega l^{2}}{R}l^{2}B_{0}$
$\frac{B_{0}^{2} \omega l}{4 R}=\frac{m l^{2}}{3}\frac{d \omega }{d t}$
$\frac{3 B^{2} l^{2}}{4 m R}t=-\displaystyle \int \frac{d \omega }{d t}$
$t=\frac{4 m R l n 2}{3 B^{2} l^{2}}$
$\therefore \text{a}=4 \, \text{and b}=3 \\ \Rightarrow \text{a}+\text{b}=4+3=7$