Question

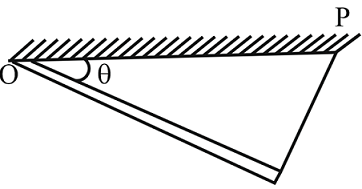
A uniform rod of mass m and length $L$ is hinged at one of its end with the ceiling and another end of the rod is attached with a thread which is attached with the horizontal ceiling at point $P$ . If one end of the rod is slightly displaced horizontally and perpendicular to the rod and released. If the time period of small oscillation is $2\pi \sqrt{\frac{2 l sin \theta }{x g}}$ . Find $x.$

Answer 1

Consider a small angular displacement $\beta $
Torque about the rotational axis
$\tau=-\left(m g \frac{l}{2} sin \theta \right) \, \left(\beta \right)$
$\tau=I\alpha $
$1=m\frac{\left(l sin \theta \right)^{2}}{3}=m\frac{l^{2} \left(sin\right)^{2} ⁡ \theta }{3}$
$-\left(m g \frac{l}{2} sin \theta \right) \, \left(\beta \right)=\frac{m l \left(sin\right)^{2} ⁡ \theta }{3} \, \alpha $
$\alpha =-\left(\frac{3 g}{2 l sin \theta }\right)\beta $
$\therefore \, \, \, T=2\pi \sqrt{\frac{2 l sin \theta }{3 g}}$