Question

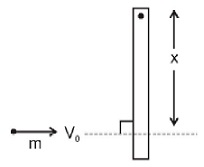
A uniform rod of mass m and length $L$ is hinged at one end and free to rotate in the horizontal plane. All the surface are smooth. A particle of same mass $m$ collides with the rod perpendicular to the length of rod with a speed $V_{0}$ . The coefficient of restitution for the collision is $e=\frac{1}{2}$ . If hinge reaction during the collision is zero then the value of $x$ is:

• A. No such value of x is possible
• B. $x=\frac{L}{2}$
• C. $x=\frac{2 L}{3}$
• D. $x=L$

Answer 1

Answer: (C)

Angular momentum conservation about the hinge

$mv_{0}x=mv_{1}x+\frac{m L^{2}}{3}\omega $
$v_{0}x=v_{1}x+\frac{\omega L^{2}}{3}$ ...(i)
$e=\frac{\omega x - v_{1}}{v_{0}}=\frac{1}{2}$ ...(ii)
Impulse of hinge
$J=m\omega \frac{L}{2}+mv_{1}-mv_{0} \, $
$J=m\omega \frac{L}{2}-m\frac{\omega L^{2}}{3 x} \, $
$J=0$
$x=\frac{2 L}{3}$
It is independent of 'e'