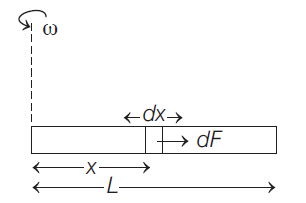
Question

A uniform rod of length $L$ is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is $\omega$. Find increase in length of the rod, if $\rho$ and $Y$ are the density and Young's modulus of the rod respectively,

• A. $\frac{\rho \omega^{3} Y}{4 L^{2}}$
• B. $\frac{4 \rho \omega^{2} L^{3}}{3 Y}$
• C. $\frac{\rho \omega^{3} L^{3}}{3 Y}$
• D. $\frac{\rho \omega^{3} L^{3}}{8 Y}$

Answer 1

Answer: (C)

Given,
length of uniform $\operatorname{rod}=L$
angular speed $=\omega$
and density of rod $=\rho$ When rod is rotated in a horizontal plane, centrifugal force is responsible for increasing the length of rod, which is also equal to stress.
If $d l$ be the change in length of small element $d x$
due to rotation, by application of force $d F$.

Young's modulus,
$ Y=\frac{\text { stress }}{\text { strain }}=\frac{d F / A}{d l / x}$
$\Rightarrow d l=\frac{d F \cdot x}{A Y} $
$\Rightarrow d F=\frac{A Y d l}{x} \,...(i)$
Where, $d F=$ centrifugal force due to mass of the
element of length, $d x$.
$d F=d m \cdot x \omega^{2} $
$d F=\frac{m}{L} \cdot x d x \omega^{2} \,...(ii)$
$\left[\because \text { Change in mass } d m=\frac{m}{L} d x\right]$
From Eqs. (i) and (ii), we get
$\frac{A Y d l}{x} =\frac{m}{L} \cdot \,x \,d x \,\omega^{2}$
$\Rightarrow d l= \frac{m x^{2} \omega^{2}}{L A Y} \cdot d x$
$\Rightarrow $ Total change in length,
$l =\int d l=\int_{0}^{L} \frac{m x^{2} \omega^{2}}{L A Y} d x$
$=\frac{m \omega^{2} L^{2}}{3 A Y}=\frac{m}{A L} \cdot \frac{\omega^{2} L^{3}}{3 Y}=\frac{\rho \omega^{2} L^{3}}{3 Y}$