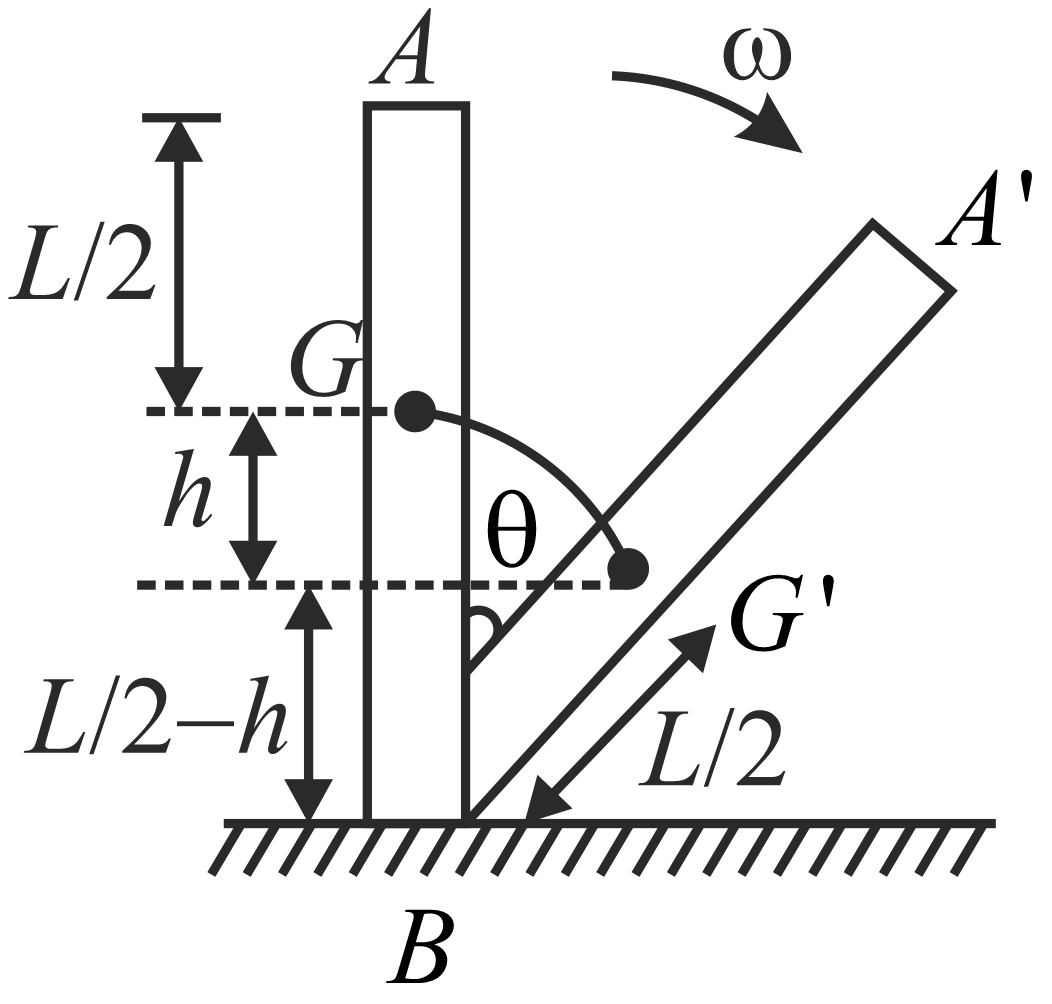
Q.
A uniform rod of length $L$ is free to rotate in a vertical plane about a fixed horizontal axis through $B$ . The rod begins rotating from rest from its unstable equilibrium position. When it has turned through an angle $\theta $ , its angular velocity $\omega $ is given by
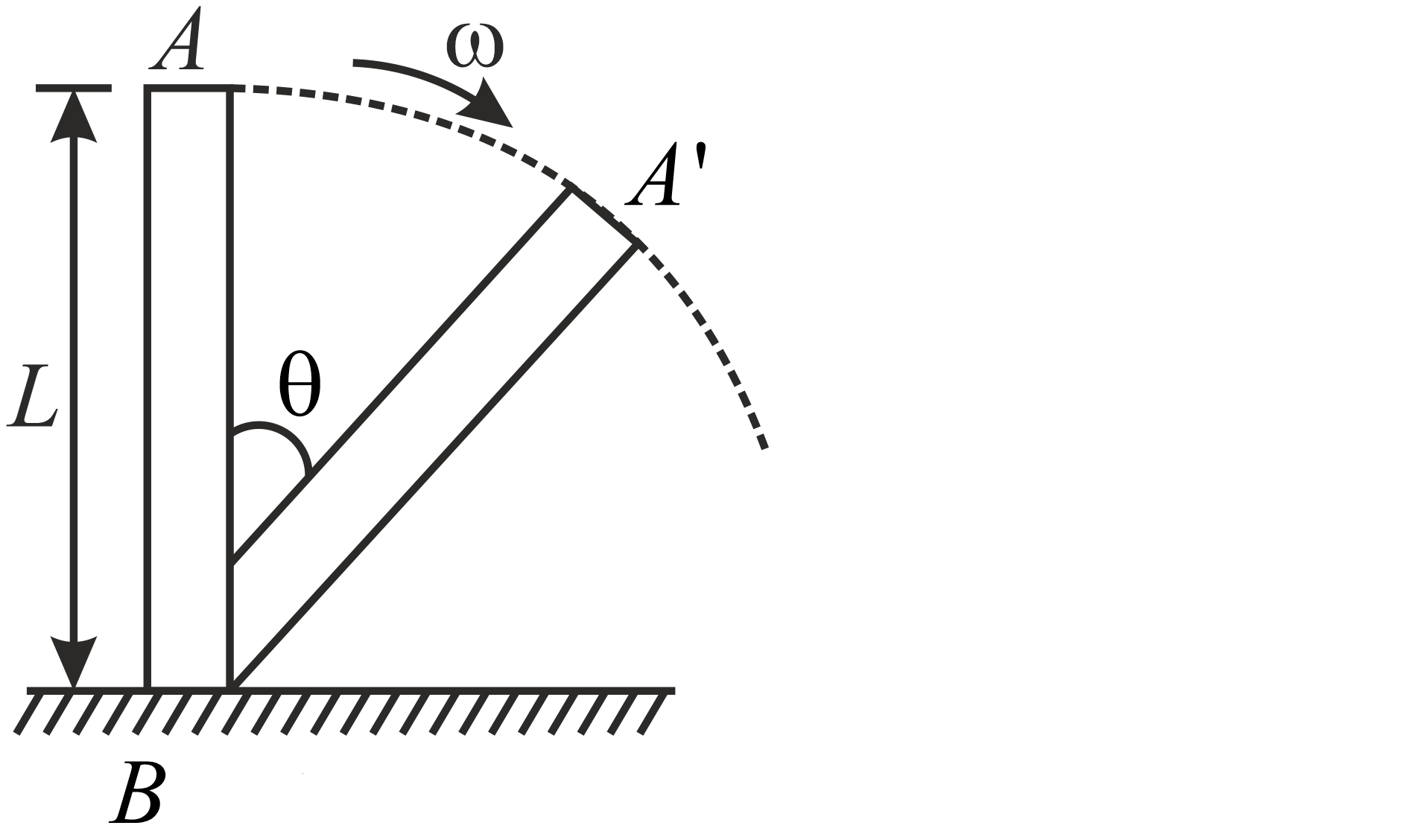
NTA AbhyasNTA Abhyas 2022
Solution: