Q.
A uniform rod of length $l$ and mass $m =1 \,kg$ is hinged at its lowest point $O$ and is connected at its highest point $A$ by means of a spring of spring constant $k$ (in fig.). When it is pushed slightly, what is the frequency of oscillation? (Take $l=2\, m , k =10$ units, $\sqrt{10}=3.14$ )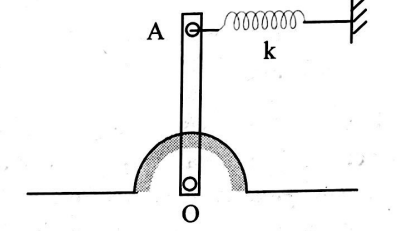
Oscillations
Solution:
