Question

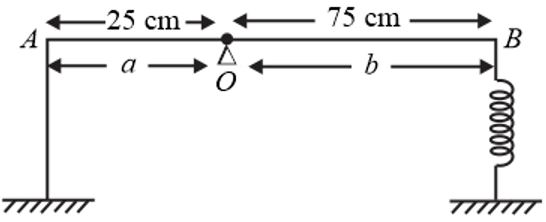
A uniform rod $AB$ of mass $2 \, kg$ and length $1 \, m$ is placed on a sharp support $O$ , such that $AO=a=25 \, cm$ and $OB=b=75 \, cm$ . A spring of force constant $600 \, N \, m^{- 1}$ is attached to the end $B$ , as shown. Initially, the spring is extended by $2 \, cm$ at equilibrium. As soon as the thread is burnt, find the normal force (in $N$ ) exerted by the support at $O$ .

Answer 1

$I$ about $O$ is $\frac{m L^{2}}{12}+\frac{m L^{2}}{16}=\frac{7 m L^{2}}{48}$
Spring force $\Rightarrow K\Delta x=600\times \frac{2}{100}=12 \, \, N$
Torque, just after burning the string,
$\tau=\left(2 \times 10 \times \frac{1}{4}\right)+12\times \frac{3}{4}$
$\Rightarrow \, \tau= \, 5 \, + \, 9 \, = \, 14 \, N \, m$
$\therefore \alpha =\frac{14 \times 48}{7 \times 2 \times 1}=48 \, rad \, s^{- 2}$
$\therefore $ Acceleration of COM,
$a=48\times \frac{1}{4}=12 \, m \, s^{- 2}$
Now, total vertical force
$12 \, + \, 20 \, - \, N \, = \, 2 \, \times \, 12$
$\Rightarrow N \, = \, 32 \, - \, 24 \, = \, 8 \, N$