Question

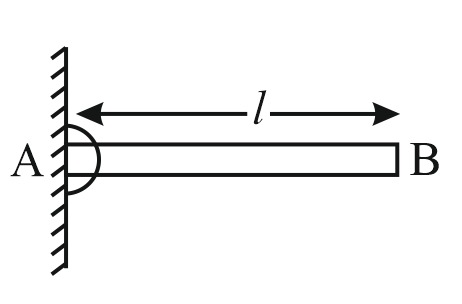
A uniform rod $AB$ of length $l$ and mass $m$ is free to rotate about point $A$ . The rod is released from rest in the horizontal position. The initial angular acceleration of the rod will be

• A. $\frac{2 \text{g}}{3 l}$
• B. $\text{g} \frac{l}{2}$
• C. $\frac{3}{2} \text{g} l$
• D. $\frac{3 \text{g}}{2 l}$

Answer 1

Answer: (D)

The moment of inertia of the uniform rod about an axis through one end and perpendicular to its length is
$\text{I} = \frac{\text{ml}^{2}}{3}$
Where m is mass of rod and l is length.
Torque $\left(\tau = \text{I} \alpha \right)$ acting on centre of gravity of rod is given by
$\tau = \text{mg} \frac{l}{2}$
or $\text{I} \alpha = \text{mg} \frac{l}{2}$
or $\frac{\text{ml}^{2}}{3} \alpha = \text{mg} \frac{l}{2}$
or $\alpha = \frac{3 \text{g}}{2 \text{l}}$