Question

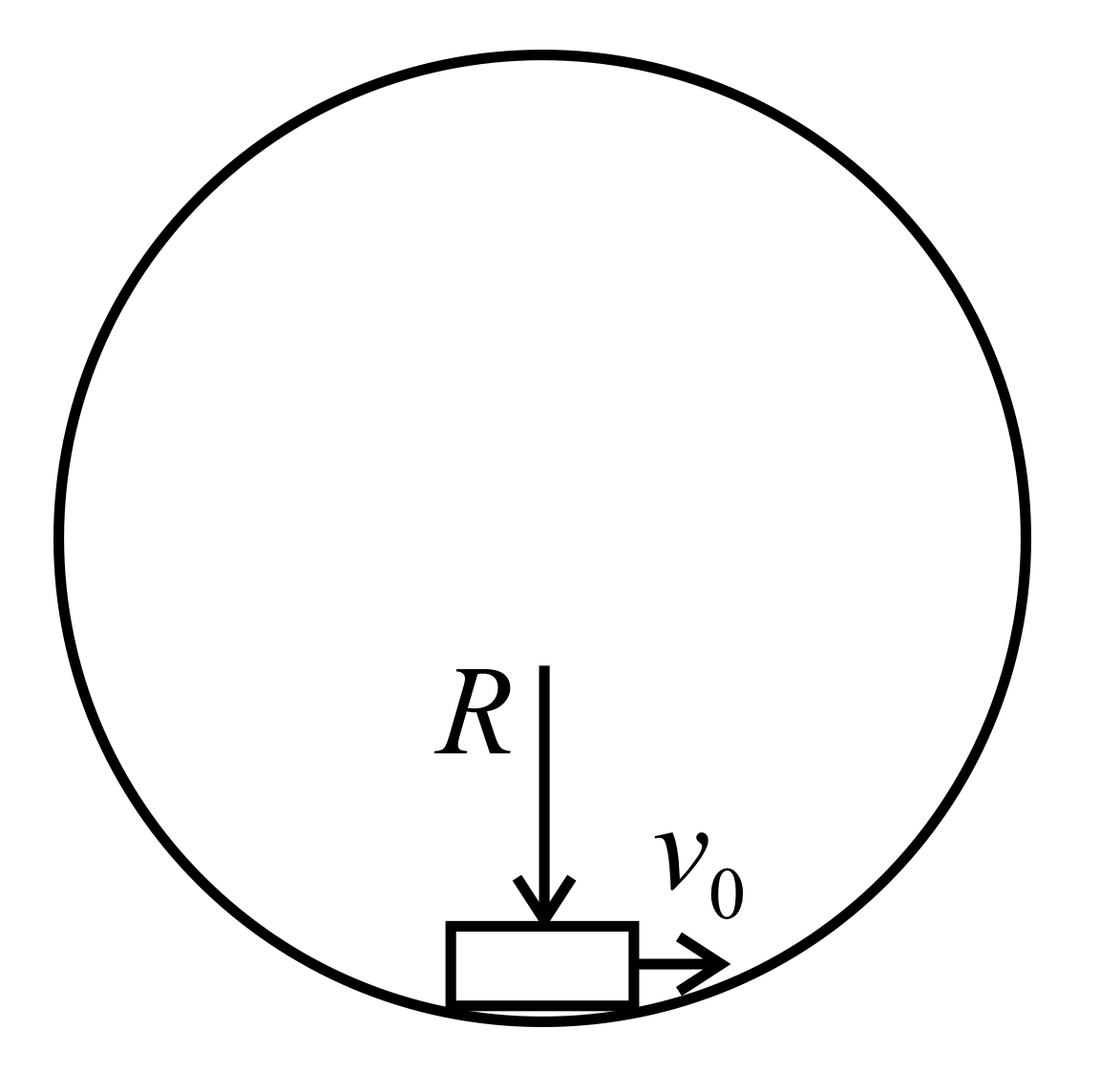
A uniform ring of mass $M$ and radius $R=1m$ is placed horizontally on a frictionless horizontal surface. A particle of mass $\frac{M}{2}$ is placed in contact with the inner side of ring as shown in the figure. What is the acceleration of the ring (in SI unit ) just after the particle is given velocity $v_{0}=9 \, m / s$ tangentially to the ring?

Answer 1

Acceleration of particle in centre of ring frame is $\frac{v^{2}}{r}$ , acceleration of centre of ring is $\frac{N}{m}$ .

$N+\frac{M}{2}a_{CM}=\frac{M v^{2}}{2 r}$
$\frac{3 M}{2}a_{c m}=\frac{M v^{2}}{2 r}$
$a_{CM}=\left(\frac{v^{2}}{3 r}\right)$
$a_{CM}=\left(\frac{9^{2}}{3 \times 1}\right)=27m\,s^{- 2}$