Q.
A uniform rectangular thin sheet $ABCD$ of mass $M$ has length $a$ and breadth $b$, as shown in the figure. If the shaded portion $HBGO$ is cut-off, the coordinates of the centre of mass of the remaining portion will be :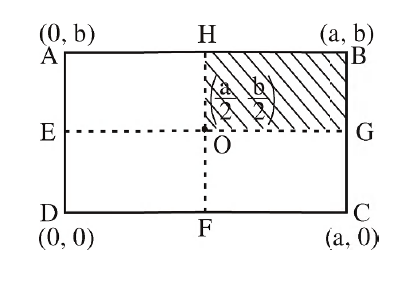
Solution:
$x = \frac{M \frac{a}{2} - \frac{M}{4} \times\frac{3a}{4}}{M - \frac{M}{4}} $
$ = \frac{\frac{a}{2} - \frac{3a}{16}}{\frac{3}{4}} = \frac{\frac{5a}{16}}{\frac{3}{4}} = \frac{5a}{12} $
$ y = \frac{M \frac{b}{2} - \frac{M}{4} \times\frac{3b}{4}}{M - \frac{M}{4}} = \frac{5b}{12} $