Question

A uniform rectangular plate $R$ of sides $a$ and $b$ and a uniform square plate $S$ of side $c$ have same masses and areas as shown in the figure.

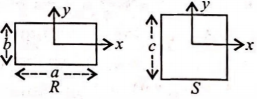
Then,
$(i) \frac{I_{xR}}{I_{xS}} < 1$
$(ii) \frac{I_{yR}}{I_{yS}} > 1$
Which of the above relations is correct?

• A. (i) only
• B. (ii) only
• C. Both (i) and (ii)
• D. Neither (i) nor (ii)

Answer 1

Answer: (C)

As, area of rectangular plate $R =$ Area of square plate $S$
$\therefore a\times b = c^2 $
$(i) \frac{I_{xR}}{I_{xS}} = \frac{b^2}{c^2} = \frac{b}{a}$
As $ b < a $
$\therefore \frac{I_{xR}}{I_{xS}} < 1$
$(ii) \frac{I_{yR}} {I_{yS}} = \frac {a^2}{c^2} = \frac{a}{b} $
As $a >b $
$\therefore \frac{I_{yR}}{I_{yS}} > 1$