Q.
A uniform metal chain of mass $m$ and length '$L$' passes over a massless and frictionless pulley. It is released from rest with a part of its length ' $l$ ' is hanging on one side and rest of its length ' $L -l$ ' is hanging on the other side of the pulley. At a certain point of time, when $l=\frac{ L }{ x }$, the acceleration of the chain is $\frac{ g }{2}$. The value of $x$ is $\ldots \ldots . .$.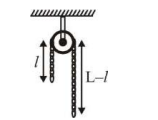
Solution:
