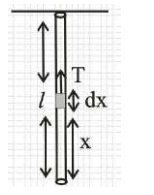
Question

A uniform heavy rod of mass $20 \, kg$. Cross sectional area $0.4 \, m ^2$ and length $20\, m$ is hanging from a fixed support. Neglecting the lateral contraction, the elongation in the rod due to its own weight is $x \times 10^{-9} m$. The value of $x$ is _______.
(Given : Young's modulus $Y =2 \times 10^{11} Nm ^{-2}$ and $g =10\, ms ^{-2}$ )

Answer 1

$ Y =\frac{ T }{ A } \frac{ dx }{ dy } $
$ m =20 \,kg $
$ A = 0 . 4 m ^2 $
$ 1=20 m$
let extension is dy in length $dx$
$Y=\frac{\text { stress }}{\text { strain }}$
$Y=\frac{\frac{T}{A}}{\frac{d y}{d x}}=\frac{T}{A} \cdot \frac{d x}{d y} $
$ d y=\frac{T d x}{A Y}$
Tension at a distance $x$ from lower end
$ =\frac{ mg }{\ell} x $
So. $ \int\limits_0^{N l} dy =\int\limits_0^{\ell} \frac{ mg }{\ell} x \frac{ dx }{ AY } $
$\Delta \ell=\frac{ mg }{\ell AY }\left[\frac{ x ^2}{2}\right]_0^{\ell}$
$\Delta \ell=\frac{ mg \ell}{2 AY }$
$ \Delta \ell=\frac{20 \times 10 \times 20}{2 \times 0.4 \times 2 \times 10^{11}}$
$ 2500 \times 10^{-11} $
$ \Delta \ell=25 \times 10^{-9} $
$=x \times 10^{-9}$
$x=25$