Q.
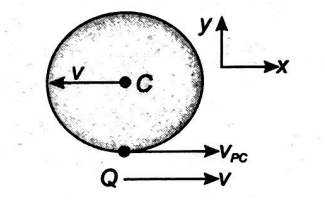
A uniform disc is spun with an angular velocity $\vec{\omega}$ and simultaneously projected with a linear velocity $v$ towards left on a plank, while the plank moves towards right with a constant velocity $2\, v$. If the disc rolls without sliding on the plank just after its spinning, the magnitude of $\vec{\omega}$ (in radian/s) is___.
(Take $v=3\, m / s , R=1\, m$ ).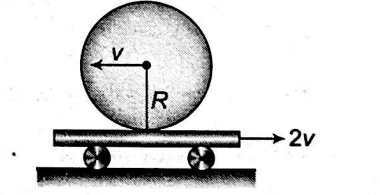
System of Particles and Rotational Motion
Solution: