Question

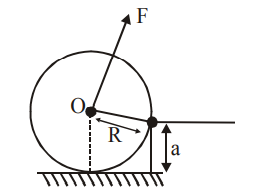
A uniform cylinder of mass $M$ and radius $R$ is to be pulled over a step of height a $(a < R)$ by applying a force $F$ at its centre $'O'$ perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure). The minimum value of $F$ required is :

• A. $Mg \sqrt{1-\frac{ a ^{2}}{ R ^{2}}}$
• B. $Mg \sqrt{\left(\frac{ R }{ R - a }\right)^{2}-1}$
• C. $Mg \frac{ a }{ R }$
• D. $Mg \sqrt{1-\left(\frac{ R - a }{ R }\right)^{2}}$

Answer 1

Answer: (D)

$(\tau)_{ P }=0$
F.R. $- mgx =0$

$x=\sqrt{R^{2}-(R-a)^{2}}$
$F = mg \frac{ X }{ R }$
$F =mg \sqrt{1-\left(\frac{ R - a }{ R }\right)^{2}}$
$=$ minimum value of force to pull