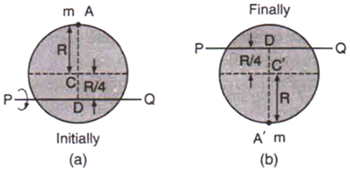
Question

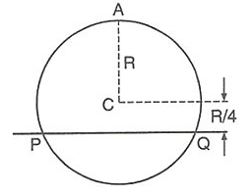
A uniform circular disc has radius $R$ and mass $m$ . A particle, also of mass $m$ , is fixed at a point $A$ on the edge of the disc as shown in the diagram. The disc can rotate freely about a fixed horizontal chord $PQ$ that is at a distance $R/4$ from the centre $C$ of the disc. The line $AC$ is perpendicular to $PQ$ .
Initially, the disc is held vertical with point $A$ at its highest position. It is then allowed to fall so that it starts rotating about $PQ$ . Find the linear speed of the particle as it reaches its lowest position.

• A. $- \sqrt{\text{2gR}}$
• B. $\sqrt{\text{3gR}}$
• C. $- \sqrt{\text{4gR}}$
• D. $\sqrt{\text{5gR}}$

Answer 1

Answer: (D)

As moment of inertia of a disc about a diameter is $\frac{1}{2}\left(\frac{1}{2} \mathrm{mR}^2\right)$
the moment of inertia of the disc about the chord PQ by 'theorem of parallel axes' will be
$\left(\mathrm{I}_{\mathrm{D}}\right)_{\mathrm{PQ}}=\frac{1}{4} \mathrm{mR}^2+\mathrm{m}\left(\frac{1}{4} \mathrm{R}\right)^2=\frac{5}{16} \mathrm{mR}^2$
and as particle of mass $m$ is at a distance $[R+(R / 4)=(5 / 4) R]$ from $P Q$,
the moment of inertia of the system about $P Q$
$\mathrm{I}=\left(\mathrm{I}_{\mathrm{D}}\right)_{\mathrm{PQ}}+\left(\mathrm{I}_{\mathrm{P}}\right)_{\mathrm{PQ}}=\frac{5}{16} \mathrm{mR}^2+\mathrm{m}\left(\frac{5}{4} \mathrm{R}\right)^2=\frac{15}{8} \mathrm{mR}^2$
Now if $w$ is the angular speed of the system when $A$ reaches the lowest point $A$ ' on rotation about the axis $P Q$, by 'conservation of mechanical energy',
$\frac{1}{2} \mathrm{I} \omega^2=\mathrm{mg}\left(\mathrm{AA}^{\prime}\right)+\mathrm{mgCC}=\mathrm{mg}\left[2 \mathrm{AD}+2 \mathrm{CD}^{\prime}\right]$

i.e., $\quad \frac{1}{2} \times \frac{15}{8} m R^2 \omega^2=2 m g\left[\left(R+\frac{1}{4} R\right)+\frac{1}{4} R\right]$,
i.e., $\omega=4 \sqrt{\frac{ g }{5 R }}$
so $\quad(\mathrm{v})_{\mathrm{A}}=\mathrm{r} \omega=\left(\mathrm{R}+\frac{1}{4} \mathrm{R}\right) \times 4 \sqrt{\frac{\mathrm{g}}{5 \mathrm{R}}}=\sqrt{5 \mathrm{gR}}$