Q.
A uniform chain of length $l$ and mass $m$ lies on the surface of a smooth hemisphere of radius $R(R>l)$ with one end tied to the top of the hemisphere as shown in the figure. Gravitational potential energy of the chain with respect to the base of the hemisphere is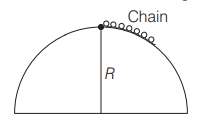
AP EAMCETAP EAMCET 2018
Solution:
