Question

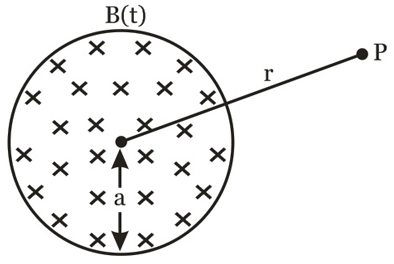
A uniform but time-varying magnetic field $B\left(\right.t\left.\right)$ exists in a circular region of radius $a$ and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point $P$ (outside the circular region) at a distance $r$ from the centre of the circular region

​

• A. Is zero
• B. Decreases as $\frac{1}{r}$
• C. Increases as $r$
• D. Decreases as $\frac{1}{r^{2}}$

Answer 1

Answer: (B)

$\displaystyle \int \overset{ \rightarrow }{E}.d\overset{ \rightarrow }{l}=\left|\right. \frac{d \phi}{d t} \left|\right.=A\left|\right. \frac{d B}{d t} \left|\right.$
$\Rightarrow $ $E\left(2 \pi r\right)=\pi a^{2}\left|\frac{\text{d} \textit{B}}{\text{d} \textit{t}}\right|$ for $r\geq a$
Therefore, $E=\frac{a^{2}}{2 r}\left|\frac{\text{d} \textit{B}}{\text{d} \textit{t}}\right|$
Therefore, the Induced electric field $ \propto \frac{1}{\text{r}}$
For $r\leq a$
$E \left(\right. 2 \pi r \left.\right) = \pi r^{2} \left|\right. \frac{d B}{d t} \left|\right.$
or
$\textit{E}=\frac{r}{2}\left|\frac{\text{d} \textit{B}}{\text{d} \textit{t}}\right|$ or $E \propto r$
At r = a, $E=\frac{a}{2}\left|\frac{\text{d} \textit{B}}{\text{d} \textit{t}}\right|$
Therefore, the variation of $E$ with $r$ (distance from centre) will be as follows: