Question

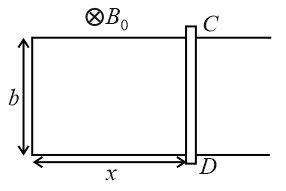
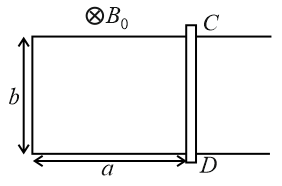
A $U$ -shaped conducting frame is fixed in space. A conducting rod $CD$ lies at rest on the smooth frame as shown. The frame is in a uniform magnetic field $B_{0},$ which is perpendicular to the plane of the frame. At the time $t=0$ , the magnitude of the magnetic field begins to change with time t as, $B=\frac{B_{0}}{1 + k t},$ where k is a positive constant. For no current to be ever induced in the frame, the speed with which rod should be pulled starting from time $t=0$ is (the rod CD should be moved such that its velocity must lie in the plane of frame and perpendicular to rod $CD$ )

• A. $ak$
• B. $bk$
• C. $a\left(1 + k t\right)$
• D. $b\left(1 + k t\right)$

Answer 1

Answer: (A)

The magnetic flux must remain constant.

$\therefore \, \, \phi_{m}=B \, bx=\frac{B_{0}}{1 + k t}bx$
Where $x$ is as shown
$\therefore \, \, \, x=a\left(1 + k t\right) \, or \, v=\frac{d x}{d t}=ak.$