Q.
A typical light dimmer, used to dim the stage lights in a theatre consists of a variable induction for $L$ (where inductance is adjustable between zero and $\left.L_{\max }\right)$, is connected in series with a light bulb $B$ as shown. The mains electrical supply is $220 \,V$ at $50\, Hz$ and the light bulb is rated at $220\, V , 1100\, W$. What $L_{\max }$ is required if the rate of energy dissipation in the light bulb is to be varied by a factor of 5 from its upper limit of $1100 \,W$ ?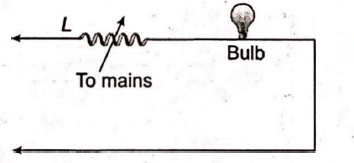
Alternating Current
Solution: