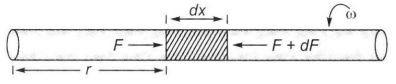
Question

A tube of length $L$ is filled completely with an incompressible liquid of mass $M$ and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity $\omega.$ The force exerted by the liquid at the other end is

• A. $\frac{1}{2} M \omega^{2} L$
• B. $\frac {ML^2 \omega}{2}$
• C. $ML \omega ^2$
• D. $\frac {ML^2 \omega^2}{2}$

Answer 1

Answer: (A)

Let the length of a small element of tube be $dx$. Mass of this element
$dm= \frac {M}{L}dx$
where $M$ is mass of filled liquid and $L$ is length of tube.
Force on this element,
$dF=dm \times x \omega^2$
$\int\limits _0^FdF= \frac {M}{L}\omega^2 \int\limits _0^Lxdx$
or $F= \frac {M}{L}\omega^2 \left[\frac {L^2}{2}\right]=\frac {ML\omega^2}{2}$
or $F=\frac {1}{2}ML\omega^2$