Q.
A trolley is moving horizontally with a constant velocity of $v( m / s )$ w.r.t. the earth. A man starts running from one end of the trolley with a velocity $1.5\, v( m / s )$ w.r.t. to trolley. After reaching the opposite end, the man returns to starting end and continues running with a velocity of $1.5 \,v( m / s )$ w.r.t. the trolley in the backward direction. If the length of the trolley is $L$, then the displacement of the man with respect to the earth during the process is $\frac{p L}{q}$. Find $(p+q)$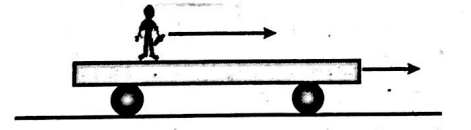
Motion in a Straight Line
Solution: