Q.
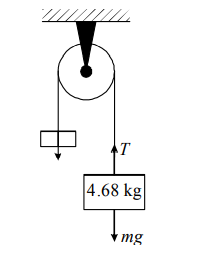
A transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves with an amplitude of $1.12\, cm$. The motion of the bar is continuous and is repeated regularly $120$ times per second. The string has linear density of $117\, g / m$. The other end of the string is attached to a mass $4.68\, kg$. The string passes over a smooth pulley and the mass attached to the other end of the string hangs freely under gravity.
The maximum magnitude of the transverse speed is :
Waves
Solution: