Q.
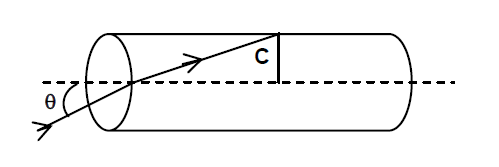
A transparent solid cylindrical rod has a refractive index of $\frac{2}{\sqrt{3}}$. It is surrounded by air. A light ray is incident at the mid point of one end of the rod as shown in the figure.
The incident angle $θ$ for which the light ray grazes along the wall of the rod is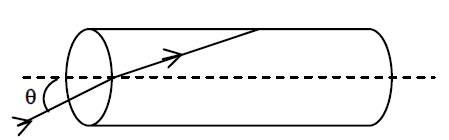
AIEEEAIEEE 2009Ray Optics and Optical Instruments
Solution:
$sinC=\frac{\sqrt{3}}{2}\,.....\left(1\right)$
$Sin \,r = sin \left(90 - C\right) = cos\,C=\frac{1}{2}$
$\frac{sin \,\theta}{sin \,r}=\frac{\mu_{2}}{\mu_{1}}$
$sin \,\theta=\frac{2}{\sqrt{3}}\times\frac{1}{2}$
$\theta=sin^{-1}\left(\frac{1}{\sqrt{3}}\right)$