Q. A train of mass $M$ is moving on a circular track of radius $R$ with constant speed $v$ . The length of train is half the perimeter of track. The linear momentum of the train will be
NTA AbhyasNTA Abhyas 2022
Solution:
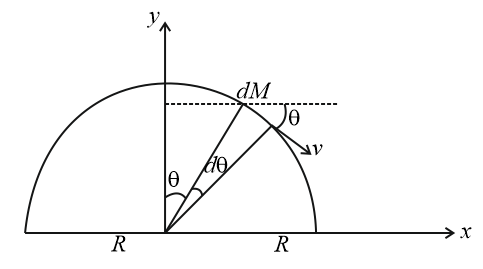
The net momentum is along the $x-$ axis, as net momentum in $y-$ axis is zero.
Momentum of the element is,
$dp=\displaystyle \int _{\theta = - 90}^{+ 90}\left(d m\right)\left(v cos \theta \right)$
Elemental mass is given by, $dm=\frac{M}{\pi R}\times Rd\theta $
Total momentum is,
$\Rightarrow p=\displaystyle \int _{- 90 ^\circ }^{90 ^\circ }\left[\left(\frac{M}{\pi R} R d \theta \right) \left(v cos \theta \right)\right]$
$\Rightarrow p=\left(\frac{M v}{\pi }\right)\displaystyle \int _{- 90 ^\circ }^{90 ^\circ }\left(cos \theta d \theta \right)=\frac{2 M v}{\pi }$

The net momentum is along the $x-$ axis, as net momentum in $y-$ axis is zero.
Momentum of the element is,
$dp=\displaystyle \int _{\theta = - 90}^{+ 90}\left(d m\right)\left(v cos \theta \right)$
Elemental mass is given by, $dm=\frac{M}{\pi R}\times Rd\theta $
Total momentum is,
$\Rightarrow p=\displaystyle \int _{- 90 ^\circ }^{90 ^\circ }\left[\left(\frac{M}{\pi R} R d \theta \right) \left(v cos \theta \right)\right]$
$\Rightarrow p=\left(\frac{M v}{\pi }\right)\displaystyle \int _{- 90 ^\circ }^{90 ^\circ }\left(cos \theta d \theta \right)=\frac{2 M v}{\pi }$