Question

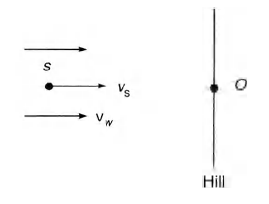
A train approaching a hill at a speed of 40 km/h sounds a
whistle of frequency 580 Hz when it is at a distance of 1 km
from a hill. A wind with a speed of 40 km/h is blowing in the
direction of motion of the train . Find
(a) the frequency of the whistle as heard by an observer on
the hill,
(b) the distance from the hill at which the echo from the hill
is heard by the driver and its frequency.
(Velocity of sound in air = 1200 km/h)

Answer 1

Given $v_s=v_w$ 40 km/h and v= 1200 km/h = speed of
sound.
(a) Frequency observed by observer $f'=f\bigg(\frac{v+v_w}{v+v_w-v_s}\bigg)$
Substituting the values, we have
$f'=580\bigg[\frac{1200+40}{1200+40-40}\bigg]=599.33\, Hz$
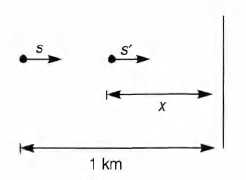
(b) Let x be the distance of the source from the hill at which
echo is heard of the sound which was produced when
source was at a distance 1 km from the hill. Then, time
taken by the source to reach from s to s' = time taken by
the sound to reach from s to hill and then from hill to s'.
Thus,
$\frac{1-x}{40}=\frac{1}{1200+40} +\frac{x}{1200-40}$
Solving this equation, we get x = 0.935km
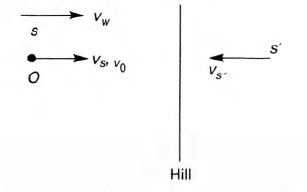
Frequency heard by the driver of the reflected wave
$f'=f \bigg[\frac{v-v_w+v_0}{v-v_w+v_s}\bigg] \, \, \, \, \, 580\bigg[\frac{1200-40+40}{1200-40-40}\bigg]=621.43\, Hz$