Q.
A track is mounted on a large wheel that is free to turn with negligible friction about a vertical axis (Fig). A toy train of mass $M$ is placed on the track and, with the system initially at rest, the train's electrical power is turned on. The train reaches speed $v$ with respect to the track. What is the wheel's angular speed if its mass is $m$ and its radius is $r ?$ (Treat it as a hoop, and neglect the mass of the spokes and hub.)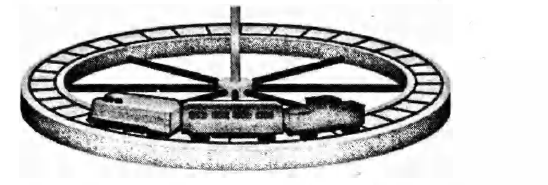
System of Particles and Rotational Motion
Solution: