Q.
A track has two inclined surface $AB$ and $DC$ each of length $3\, m$ and angle of inclination of $30^°$ with the horizontal and a central horizontal part of length $4\, m$ as shown in figure. A block of mass $0.2\, kg$ slides from rest from point $A$. The inclined surfaces are frictionless. If the coefficient of friction between the
block and the horizontal flat surface is $0.2$, where will the block finally come to rest ?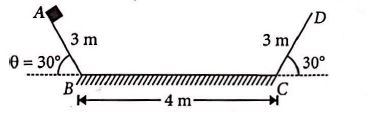
Work, Energy and Power
Solution:
