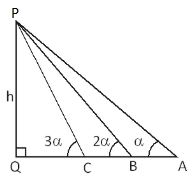
Question

A tower subtends angles $\alpha , \, 2\alpha $ and $3\alpha $ respectively at points, $A,B$ and $C$ (all points lying on the same side on a horizontal line through the foot of the tower), then the value of $\frac{A B}{B C}$ is equal to

• A. $1+2cos 2 \alpha $
• B. $1-2cos 2 \alpha $
• C. $1+3cos 2 \alpha $
• D. $1-3cos 2 \alpha $

Answer 1

Answer: (A)

Let, the height of the tower is $PQ=h$
Where, $Q$ is the foot of the tower and $P$ is the top of the tower, then
$QA=hcot \alpha $
$QB=hcot 2 \alpha $
$QC=hcot 3 \alpha $

$\frac{A B}{B C}=\frac{Q A - Q B}{Q B - Q C}=\frac{cot \alpha - cot ⁡ 2 \alpha }{cot ⁡ 2 \alpha - cot ⁡ 3 \alpha }$
$=\frac{\frac{cos \alpha }{sin ⁡ \alpha } - \frac{cos ⁡ 2 \alpha }{sin ⁡ 2 \alpha }}{\frac{cos ⁡ 2 \alpha }{sin ⁡ 2 \alpha } - \frac{cos ⁡ 3 \alpha }{sin ⁡ 3 \alpha }}=\frac{sin ⁡ 2 \alpha cos ⁡ \alpha - cos ⁡ 2 \alpha sin ⁡ \alpha }{sin ⁡ 3 \alpha cos ⁡ 2 \alpha - cos ⁡ 3 \alpha sin ⁡ 2 \alpha }\times \frac{sin ⁡ 3 \alpha }{sin ⁡ \alpha }$
$=\frac{sin 3 \alpha }{sin ⁡ \alpha }=3-4sin^{2}\alpha =1+2cos⁡2\alpha $