Question

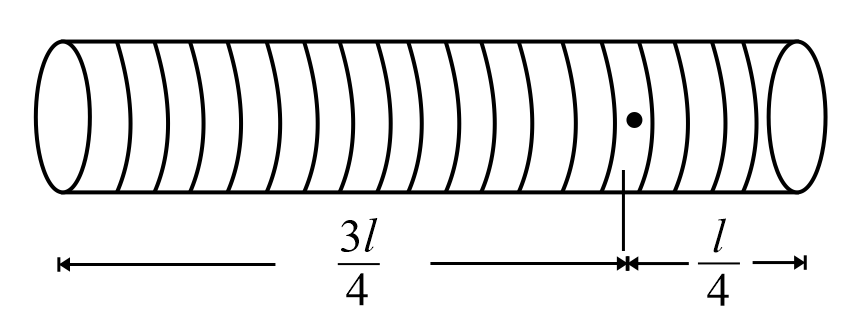
A tightly wound solenoid of radius $‘a’$ and length $‘l’$ has $n$ turns per unit length. It carries an electric current $i$ . Magnetic field at a distance $\frac{l}{4}$ from one of the end (inside the solenoid on its axis) is $B=\frac{\left(\mu \right)_{0} n i \left(\sqrt{5} + 3\right)}{\sqrt{K}}$ for $l=4a$ . Find the value of $K$ .

Answer 1

Magnetic field inside the solenoid, $B=\frac{\mu_{0} n i}{2}\left[\sin \left(\theta_{1}\right)+\sin \left(\theta_{2}\right)\right]$
$ \sin \left(\theta_{1}\right)=\frac{3 a}{\sqrt{(3 a)^{2}+a^{2}}}=\frac{3}{\sqrt{10}} $
$ \sin \left(\theta_{2}\right)=\frac{a}{\sqrt{a^{2}+a^{2}}}=\frac{1}{\sqrt{2}} $

$\Rightarrow \quad B=\frac{\mu_{0} n i}{2}\left[\frac{1}{\sqrt{2}}+\frac{3}{\sqrt{10}}\right]$
$\Rightarrow B=\frac{\mu_{0} n i(\sqrt{5}+3)}{\sqrt{40}}$
$\therefore K=40$