Q.
A thin wire of length of $99\, cm$ is fixed at both ends as shown in the figure. The wire is kept under a tension and is divided into three segments of lengths $I_{1}, I_{2}$ and $I_{3}$ as shown in figure. When the wire is made to vibrate, the segments vibrate respectively with their fundamental frequencies in the ratio $1: 2: 3$. Then, the lengths $I_{1}, I_{2}$ and $l_{3}$ of the segments respectively are (in $cm$ )
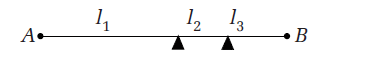
TS EAMCET 2015
Solution:
