Question

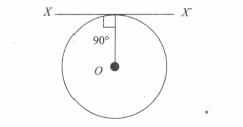
A thin wire of length $L$ and uniform linear mass density $\rho $ is bent into a circular loop with centre $O$ as shown. The moment of inertia of the loop about the axis $XX'$ is

• A. $\frac{\rho L^{3}}{8 \pi ^{2}}$
• B. $\frac{\rho L^{3}}{16 \pi ^{2}}$
• C. $\frac{5 \rho L^{3}}{16 \pi ^{2}}$
• D. $\frac{3 \rho L^{3}}{8 \pi ^{2}}$

Answer 1

Answer: (D)

Length of the wire $=L$
Density of the wire $=\rho $
Mass of the wire and hence of the loop is, $M=\rho L$
and radius of the loop is, $r=\frac{L}{2 \pi }$

Moment of inertia of a ring about an axis passing through its center and lying in its plane, $I_{1}=\frac{M r^{2}}{2}$
Using parallel axis theorem, we can say that
$I_{2}=I_{1}+Mr^{2}$
$\Rightarrow I_{2}=\frac{M r^{2}}{2}+Mr^{2}$
$\Rightarrow I_{2}=\frac{3 M r^{2}}{2}$
$\Rightarrow I_{2}=\frac{3}{2}\left(\rho L\right)\left(\frac{L}{2 \pi }\right)^{2}$
$\Rightarrow I_{2}=\frac{3 \rho L^{3}}{8 \pi ^{2}}$