Q.
A thin walled glass sphere of radius $2.5\, cm$ is filled with water. An object $(O)$ is placed at $7.5\, cm$ from the surface of the sphere. Neglecting the effect of glass wall, at what distance the image $(I)$ of the object, measured from the centre of sphere is formed?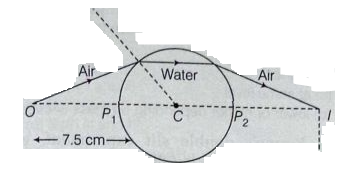
ManipalManipal 2016
Solution: