Question

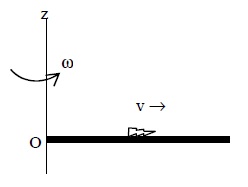
A thin uniform rod,pivoted at O, is rotating in the horizontal plane with constant angular speed ω, as shown in the figure. At time t = 0, a small insect starts from O and moves with constant speed v,with respect to the rod towards other end. It reaches the end of the rod at t = T and stops.The angular speed of the system remains ω throughout. The magnitude of the torque $\left(\left|\overset{ \rightarrow }{\tau}\right|\right)$ about O,as a function of time is best represented by which plot?

• A.
• B.
• C.
• D.

Answer 1

Answer: (B)

angular momentum
$\mathrm{J}=\mathrm{IW} \mathrm{z}=\frac{\mathrm{dJ}}{\mathrm{dt}}=\mathrm{w} \frac{\mathrm{dI}}{\mathrm{Dt}} \\ {\left[\mathrm{I}=\mathrm{I}_{\mathrm{rod}}+\mathrm{I}_{\mathrm{insect}}\right.} \\ \left.=\mathrm{C}+\mathrm{mr}^2 \Rightarrow \mathrm{c}+\mathrm{m}(\mathrm{vt})^2\right] \\ \tau=\omega \frac{\mathrm{dI}}{\mathrm{dt}}=\omega \frac{\mathrm{d}}{\mathrm{dt}}\left(\mathrm{C}+\mathrm{mv}^2 t^2\right) \\ =\mathrm{m} \omega \mathrm{v}^2 2 t \\ $
So, the graph between $|\tau|$ and $t$ is straight line.