Question

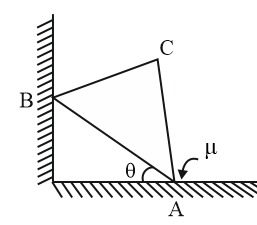
A thin uniform equilateral plate rests in a vertical plane with one of its vertex $A$ on a rough horizontal floor and another vertex $B$ on a smooth vertical wall. If the coefficient of friction $\mu =\frac{1}{\sqrt{3}}$ , then the least angle $\theta $ its base $AB$ can make with the horizontal surface is

• A. $\theta =cot^{- 1}\left[\mu + \frac{1}{\sqrt{3}}\right]$
• B. $\theta =tan^{- 1}\left[\mu + \frac{1}{\sqrt{3}}\right]$
• C. $\theta =tan^{- 1}\left[2 \mu + \frac{1}{\sqrt{3}}\right]$
• D. $\theta =cot^{- 1}\left[2 \mu + \frac{1}{\sqrt{3}}\right]$

Answer 1

Answer: (D)

Let us assume that the side-length of the triangle is $a$ , then
$l=\frac{a}{\sqrt{3}}$
$N_{1}=Mg$
$f_{1}=\mu N_{1}=N_{2}$
$N_{2}=\mu Mg$
Balancing the torque about point $A$
$Mg\times lcos\left(30 ^\circ + \theta \right)-N_{2}\times asin\theta =0$
$\Rightarrow Mg\times \frac{a}{\sqrt{3}}cos\left(30 ^\circ + \theta \right)-\mu Mg\times asin\theta =0$
$\frac{1}{\sqrt{3}}\left(\frac{\sqrt{3}}{2} cos \theta - \frac{1}{2} sin \theta \right)=\mu sin\theta $
On solving further we get
$\theta =cot^{- 1}\left[2 \mu + \frac{1}{\sqrt{3}}\right]$