Q.
A thin uniform annular disc (see figure) of mass $M$ has outer radius $4R$ and inner radius $3R$. The work required to take a unit mass from point $P$ on its axis to infinity is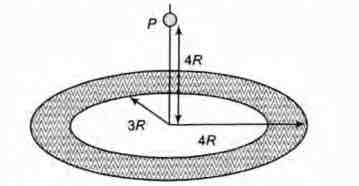
IIT JEEIIT JEE 2010Gravitation
Solution:
$W =\Delta U = U_f -U_i =U_{\infty} -U_P = -U_P =- m V_P $
$ \, \, \, \, \, \, \, \, \, \, \, = - V_P \, \, \, \, \, \, \, \, \, \, \, \, \, \, (as m=1) $
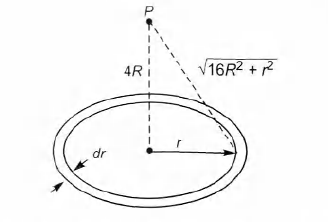
Potential at point P will be obtained by integration as given below.
Let dM be the mass of small ring as shown
$dM = \frac{ M}{ \pi (4 R) ^2 - \pi (3R)^2} (2 \pi r ) dr = \frac{2Mr dr }{ 7 R^2}$
$ dV_P = - \frac{G dM}{\sqrt{16 R^2 +r^2}} = - \frac{ 2GM}{ 7 R^2} \int \limits_{3R}^{4R} \frac{r}{ \sqrt{16 R^2 +r^2 }} dr $
$= - \frac{2GM}{ 7R} (4 \sqrt 2 -5 )$
$\therefore \, \, \, \, \, \, \, W = + \frac{ 2GM}{7R} (4 \sqrt 2 - 5 )$
$\therefore \, \, \, \, \, $ Correct option is (a).